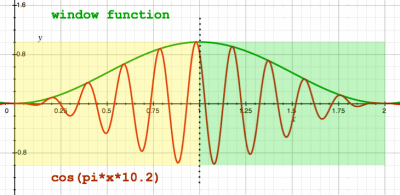
Below, I have done a visual impression of such signal wrapping. Notice that the window stretches over two subsequent signal blocks.

The second block is wrapped over the first one, summing the sample values, and the total is put in one FFT analysis.

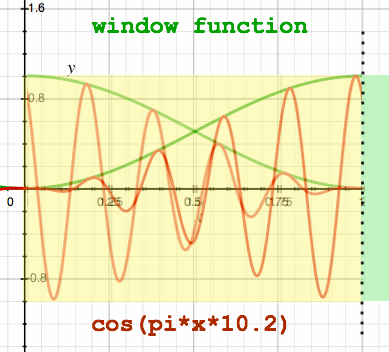From the figure, it seems that the function as it appears to the FFT, is now periodical. Here is another impression of signal wrapping, with the samples summed in the third figure:

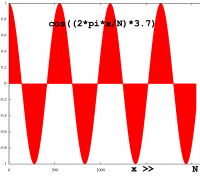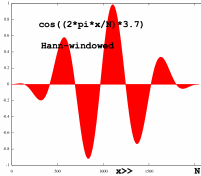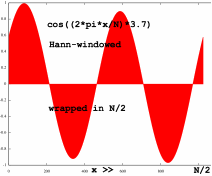Ok, it is now periodical within the FFT frame, but it is not 1 frequency anymore, since it is modulated. Let me check what the spectrum looks like. Maybe not so surprising, it is similar to the N-point spectrum of the original input, only the wrapped version is compressed to a N/2 point spectrum.

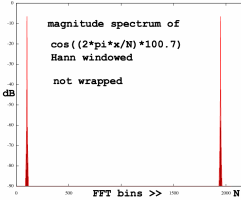Notice the difference in size. Accounting for it's N/2 spectrum size, the wrapped version has a remarkable leakage character. In terms of unit bin width, the main lobe is reduced to half size: two bins instead of the four bins that are normally associated with a Hann window. It is really the N-point spectrum translated to N/2 point resolution: a factor 2 downsampling of the spectrum. It is the opposite of the zero-padding that I used to generate the upsampled spectra on the previous page, to inspect the Dirichlet functions.

What is the use of this spectrum downsampling? Would we not rather need a more accurate spectrum instead of a less accurate one? Well... since the windowed Fourier transform of a pure sinusoid is by definition a Dirichlet sum with four coefficients in it's main lobe, why not just summarize these in a spectrum of lesser resolution? It reduces the risk of accidentally chopping a main lobe with a sharp filter.

To improve the leakage character, an extra window function is applied. It is a sinc function: FFTsize*(sin(pi*x/FFTsize)/(pi*x)). Because the periodicity of the sinc function is dependent on the FFT frame size and not the input block size, the resulting window function depends on how much of the input you want to wrap in one FFT analysis frame:

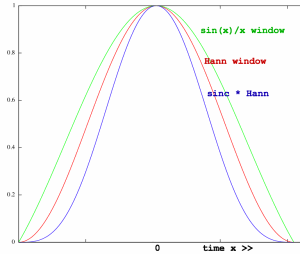inputblock = FFTsize*2

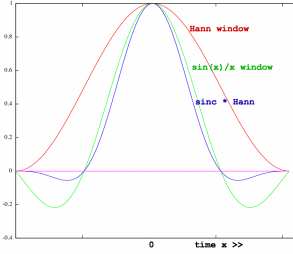inputblock = FFTsize*4

These windows do not produce a constant sum when they are overlapped. Without demodulation, it would look like this:

inputblock = FFTsize*4